A CASE STUDY IN REPRESENTING SCIENTIFIC
APPLICATIONS (GeoAc) USING
THE SPARSE POLYHEDRAL FRAMEWORK

by
Ravi Shankar

 

A thesis
submitted in partial ful llment
of the requirements for the degree of
Master of Science in Computer Science
Boise State University
August 2021

 

©2021
Ravi Shankar
ALL RIGHTS RESERVED

 

BOISE STATE UNIVERSITY GRADUATE COLLEGE

DEFENSE COMMITTEE AND FINAL READING APPROVALS

 

of the thesis submitted by

Ravi Shankar

Thesis Title: A Case Study in Representing Scienti c Applications (GeoAc) using the Sparse Polyhedral Framework

Date of Final Oral Examination:   24th May 2021

The following individuals read and discussed the thesis submitted by student Ravi Shankar, and they evaluated the presentation and response to questions during the final oral examination. They found that the student passed the final oral examination.

Catherine Olschanowsky, Ph.D.     Chair, Supervisory Committee
Dylan Mikesell, Ph.D.                    Member, Supervisory Committee
Steven Cutchin, Ph.D.                    Member, Supervisory Committee

 

The nal reading approval of the thesis was granted by Catherine Olschanowsky, Ph.D., Chair of the Supervisory Committee. The thesis was approved by the Graduate College.

 

Dedicated to my family.

ACKNOWLEDGMENTS

The author would like to express gratitude to his advisor Dr. Catherine Olschanowsky for her unwavering support, encouragement and belief in him. Her patience, advice and motivation over the years have been invaluable.
The author would like to thank his supervisory committee members Dr. Dylan Mikesell and Dr. Steven Cutchin for their feedback and support. The author would also like to acknowledge the help and collaboration of current
and former members of the ADaPT Data Flow Optimizations lab especially Aaron Orenstein, Anna Rift, Tobi Popoola and Dr. Eddie Davis. This material is based upon work supported partially by the National Science
Foundation under Grant Numbers 1849463 and 1563818. Any opinions, ndings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily re ect the views of the National Science Foundation. This research utilized the high-performance computing support of the R2 compute cluster (DOI: 10.18122/B2S41H) provided by Boise State Universitys Research Computing Department.

ABSTRACT

Tsunami detection and forecasting is a di cult problem that scientists are trying to tackle. Early path estimation and accurate prediction of the arrival time and size of a tsunami can save lives and help with impact assessment. Tsunami inducing earthquakes cause ground and sea-surface displacements that push up on the atmosphere. This atmospheric disturbance propagates upwards as an acoustic wave and eventually hits the ionosphere. IonoSeis is a software simulation package that leverages satellite-based ionospheric remote-sensing techniques to determine the epicenter of these earthquakes. The execution time of the ray-tracing component of IonoSeis prevents its use as a real-time modeling tool. A proposed solution is to replace this component with a newer ray-tracing package developed by Los Alamos National Laboratory called GeoAc and parallelize it. This research is a case study that uses the sparse polyhedral framework (SPF) to represent the operational GeoAc code and thereby drive the requirements for a SPF optimization framework that is being actively developed.

 

TABLE OF CONTENTS

ABSTRACT………………………………………..
LIST OF TABLES……………………………………
LIST OF FIGURES…………………………………..
LIST OF ABBREVIATIONS ……………………………
LIST OF SYMBOLS ………………………………….

1 Introduction………………………………………

1.1 Problem Statement. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Contributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Organization. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2 Background ………………………………………

2.1 IonoSeis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 GeoAc. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Memory Optimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Optimization Frameworks. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.1 The Polyhedral Model. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.2 The Sparse Polyhedral Framework(SPF). . . . . . . . . . . . . . . . . .
2.4.3 The Computation API . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3 Engineering update of GeoAc …………………………

3.1 Parallelizing GeoAc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.1 Performance Pro ling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.2 Identify Candidate Loops . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.3 Refactor to prepare for Open MP . . . . . . . . . . . . . . . . . . . . . . . .
3.1.4 Implementation and Testing . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.5 Performance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Up grading data formats to industry standards. . . . . . . . . . . . . . . . . . . .
3.2.1 The Network Standard Data Format(NetCDF). . . . . . . . . . . . .

4 Representing Geo Acusingthe SPF …………………….

4.1 Iterative Development . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 FunctionInlining . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Data-dependent Early Loop Exits . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4 Rewrite code using the SPF. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 5 RelatedWork …………………………………….

5.1 Applying polyhedral optimizations to scientific applications . . . . . . . . .

6 Conclusion……………………………………….

REFERENCES………………………………………
A Experimental Setup ………………………………..

 

LIST OF TABLES

3.1 Performance results of parallelized GeoAc . . . . . . . . . . . . . . . . . . . . . . .

 

LIST OF FIGURES

1.1 Satellite-based remote sensing techniques detect tsunami induced ionospheric disturbances. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.1 Flow diagram for the IonoSeis modeling frame work. Red ovals indicate model inputs,and blue boxes indicate model inputs, and blue boxes indicate individual steps that each have their own BASH script with in put parameters for that step[16].. . . . . .

2.2 An simplified loop nest from the GeoAc codebase.. . . . . . . . . . . . . . . . .

2.3 The iteration space: statements of the loop-nest in Figure 2.2 can be viewed as lattice points on a polyhedron. . . . . . . . . . . . . . . . . . . . . . . . .

2.4 Dense Matrix Vector Multiply. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.5 Sparse Matrix Vector Multiply. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.6 Computation data space setup. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.7 Partial specification of a statement using the Computation API.. . . . . .

2.8 Data dependences between statements. . . . . . . . . . . . . . . . . . . . . . . . . .
2.9 A statements execution schedule. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.10 Computation API specification for dense and sparse matrix vector multiply . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

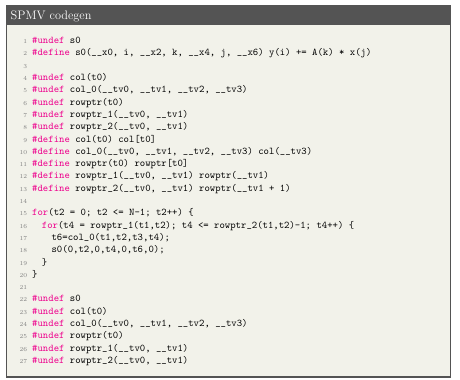
2.11Sparse matrix vector multiply C code generated by calling codegen on the Computation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.1 GeoAcs dot graph. Functions where most time is spent are marked as saturated red, and functions where little time is spent are marked as dark blue. Functions where negligible or no time is spent do not appear in the graph by default. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

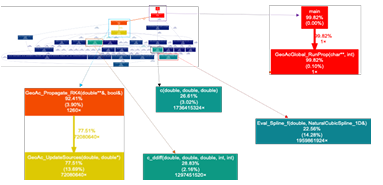
3.2 Zoomed in sections of Geo Acsdot graph identifying potential performance bottlenecks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

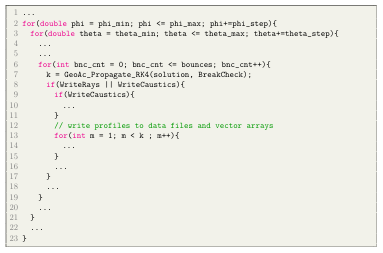
3.3 Candidate Loops. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4 Combining the global variables in to a struct. . . . . . . . . . . . . . . . . . . . .

3.5 Test parameters for Geo A cs performance study. . . . . . . . . . . . . . . . . . .

3.6 GeoAcs average run time measured over four runs for varying number of threads .Loweris better. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.7 Geo Acs speed up measured over four runs for varying number of threads. Higher is better. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3.8 The structureof the resultingNetCDF le fromGeoAc represented usingCDL. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.1 The append Computation function.. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 A nested function call using append Computation. . . . . . . . . . . . . . . . . .
4.3 The original Find Segment function in the G2SGlobal Spline1D.cpp compilation unit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.4 The modified Find Segment function to take care of early exits and return statements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5 A statement in the Find Segment Computation. . . . . . . . . . . . . . . . . . .
4.6 The data reads and writes of the Find Segment. . . . . . . . . . . . . . . . . . .
4.7 The execution schedule of  the Find Segment Computation.. . . . . . . . . .

4.8 The complete Find Segment Computation function . . . . . . . . . . . . . . . .

4.9 Code generated for a single call to the c function from the GeoAc Update Sources function results in the Computation expressed as macros. The macro s12 on line 14 represents the Find Segment function. . . . . . . . . . . . . .

4.10 Calls to the macros defined in Figure 4.9. Line 13 represents the call to the Find Segment function. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

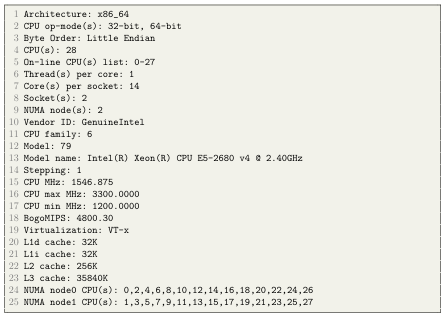
A.1 The lscpu command displays the CPU architecture information of R2.

 

LIST OF ABBREVIATIONS

CDL-

Common Data Language

GNSS-

Global Navigation Satellite Systems

IEGenLib –

Inspector/Executor Generator Library

AND –

Intermediate Representation

LANL-

Los Alamos National Laboratory

NetCDF –

Network Common Data Form

NUMA-

Non-Uniform Memory Access

ODE –

Ordinary Differential Equation

PDFG –

Polyhedral Data ow Graph

SAC –

Seismic Analysis Code

SPF –

Sparse Polyhedral Framework

WASP3D-

Windy Atmospheric Sonic Propagation

LIST OF SYMBOLS

Logical and
Set theory notation- such that
Set theory notation- A set

 

CHAPTER 1

INTRODUCTION

Tsunami detection and forecasting is a difficult problem that scientists are trying to tackle. The unpredictability of tsunamis make it difficult for early warning and evacuation of at-risk coastlines. Early estimation and accurate prediction of the arrival time and size of a tsunami can save lives and help with impact assessment to
buildings and infrastructure.

Analysis of satellite-based sensing data may help predict tsunami behaviour. Tsunami-inducing earthquakes cause ground and sea-surface displacements that push on the atmosphere, and propagate through the atmosphere into the ionosphere. Global Navigation Satellite Systems (GNSS) monitor ionospheric disturbances induced by such phenomena. Such satellite-based remote sensing techniques can be used to estimate the earths surface deformation and predict the arrival time of a tsunami. IonoSeis [16] is a software simulation package that leverages these techniques to determine the epicenter of earthquakes that could cause these tsunamis.

There are a few key areas where IonoSeis can be improved. One of its key components is a three-dimensional ray-tracing package called the Windy Atmospheric Sonic Propagation (WASP3D). WASP3D models waves arriving in the ionosphere from the epicenter of an earthquake. This ray-tracing package is currently not fast enough to meet the needs of the work ow and inhibits real-time monitoring application. There

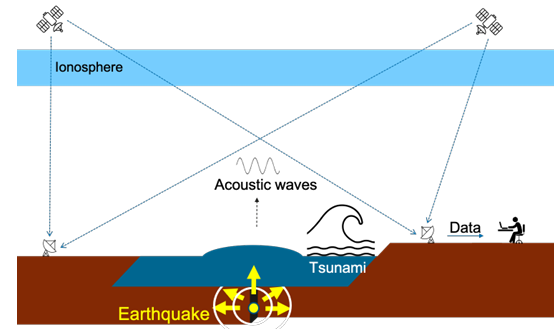
are also no provisions to simulate many potential epicenters simultaneously. One of the objectives of this thesis replaces this component of IonoSeis with the GeoAc [2] modelling tool. GeoAc is a newer ray-tracing package developed by Los Alamos National Labora tory (LANL) that more accurately models wave propagation phenomena compared to the WASP3D,the current ray-tracing model in IonoSeis. However, the execution time
of GeoAc is also too long. Scienti c applications like GeoAc are often memory-bound, requiring large amounts of memory, and spend a signi cant amount of execution time reading and writing data. This can signi cantly a ect performance. Shared memory parallelization was used within GeoAc to meet the needs of IonoSeis work ow and potentially permit real-time monitoring of tsunami hazards.

Several transformation frameworks have been developed to optimize memory bound applications. However, they su er from usability and expressivity limitations. One such framework is the sparse polyhedral framework. Tools like the SPF are used to express sparse computations and apply transformations automatically. This case study drives the development of a SPF optimization framework to enable the use of compiler transformations for performance optimization to be more expressive and therefore more usable.

1.1 Problem Statement

The execution time of the ray-tracing component of IonoSeis is not fast enough to meet the needs of the work ow and prevents its use as a real-time modelling tool. The proposed replacement to this ray-tracing component is memory-bound and spends a signi cant amount of time reading and writing data thereby a ecting performance. SPF tools su er from a lack of expressiveness that captures the true behavior of scientific applications.

1.2 Contributions

This thesis presents a case-study that drives the development of a SPF optimization framework. The optimization framework enables the use of compiler transformations for performance optimization in other scienti c applications. WASP3D, the ray-tracing component of IonoSeis is replaced with an OpenMP implementation of LANLs GeoAc acoustic ray-tracing tool. The tool was customized to meet the requirements of the work ow and generates NetCDF data les required by subsequent steps in IonoSeis.

Aperformance study was conducted with varying threads on the OpenMP implementation of GeoAc comparing run-times and speed-ups with different thread counts.

1.3 Organization

This thesis is organized as six chapters with a varying number of sections. Chapter 2 provides an overview of the domain science software tools and background information on high performance computing concepts. Chapter 3 details the software engineering e ort to parallelize GeoAc using OpenMP and customize it to meet the needs of the work ow. Chapter 4 covers the e orts to represent GeoAc using the SPF and thereby drive the optimization framework. Chapter 5 contains a review of related work. Chapter 6 concludes this thesis and provides a summary of this work.

 

CHAPTER 2

BACKGROUND

This chapter provides an overview of the domain science software tools that this research is built on, background information on high performance computing concepts, and the optimization framework that this case study drives. Section 2.1 provides an overview of the IonoSeis software simulation package and details how the ray-tracing component WASP3D does not meet the needs of the work ow and inhibits real-time monitoring application. Section 2.2 introduces the GeoAc software package that is used to replace WASP3D and is then optimized. Section 2.3 talks about the memory wall and how memory performance is a constraint in scienti c computing. Section 2.4 explores the polyhedral and sparse polyhedral compiler optimization frameworks and introduces the Computation API [21].

2.1 IonoSeis

Many earthquakes cause sudden mass displacements at the earths surface. When this type of earthquake occurs under the ocean, is of strong enough magnitude, and meets certain other criteria, a tsunami is generated. Ground or sea-surface displacements push on the atmosphere, which in turn generates an atmospheric disturbance. This disturbance propagates upward as an acoustic wave eventually inducing a local change in the electron density of the ionosphere. Global Navigation Satellite Systems (GNSS) monitor ionospheric disturbances induced by such phenomena. Such satellite-based remote sensing methods are used to estimate the earths surface deformation and predict the arrival time of a tsunami. IonoSeis is a software package that combines multiple existing codebases into a single package to model GNSS-derived electron perturbations in the ionosphere due to the interaction of the neutral atmosphere and charged particles in the ionosphere. Running IonoSeis is a 5 step process as indicated in Figure 2.1. The Seismic Analysis

Code (SAC) data format indicated by the green oval under step 5 Figure 2.1 is used to store the electron perturbation time series. Network Common Data Form (NetCDF)
les are used to store grid information between each step. WASP3D is one of the key components of IonoSeis and is a three-dimensional ray-tracing software in spherical coordinates. It is, however, an older codebase and has certain limitations:
• The execution time is not fast enough to to meet the needs of IonoSeis and inhibits real-time monitoring application.
• There are no provisions to simulate many potential epicenters simultaneously. Currently only a single epicenter can be simulated at a time.
• WASP3D does not accurately represent the physics of wave propagation.

-It does not account for viscous energy dissipation or wave ampli cation due to the rare ed atmosphere at high altitudes.
-It cannot model ionospheric perturbations greater than 500-600 km until the sampling of the atmosphere by shooting rays at nonlinear intervals can be improved.

-It does not model nonlinear waveform behavior.
-It only models in spherical coordinates. While this is useful for IonoSeis, scientists would like to be able to extend the package so that national labs that study explosives and other local acoustic sources can use a Cartesian
version of the code.

A preliminary contribution of this thesis replaces WASP3D with GeoAc

2.2 GeoAc

GeoAc [2] is a ray-tracing software tool developed at Los Alamos National Lab oratory. The software is written in C++ and is used to model the propagation of  acoustic waves through the atmosphere using a fourth-order RungeKutta (RK4) method. GeoAc models propagation in an azimuthal plane and include methods to use a Cartesian coordinate system as well as a spherical coordinate system [2]. One of the contributions of this thesis is to explore the feasibility of using an optimized version of GeoAc to perform ionospheric ray-tracing and potentially run in real-time.

A performance analysis described in Section 3.1.1 indicates that the RK4 function is the most expensive operation in GeoAc and is therefore chosen for further analysis and optimization. Figure 3.2 shows the potential performance  bottlenecks. RungeKutta methods are a family of iterative solutions commonly used to approxi mate solutions to initial value problems of ordinary di erential equations (ODEs) [30, 1]. The fourth-order Runge Kutta method is the most widely used method of solving ODEs. It is commonly used as a solver in many frame works  and libraries, providing a balance between computational cost and accuracy.

An ODEisadi erential equation specifying the relationship between a dependent variable, y, and an independent variable, x as show in in Equation 2.1. The term ordinary indicates that it has an ordinary derivative rather than a partial derivative.

dy by dx +xy =0    (2.1)

ODEs are used to model problems in engineering and various sciences that involve the change of some variable with respect to another. Most of these problems require the solution of an initial value problem. An initial value problem is an ODE together with an initial condition that speci es the value of the unknown function at some given point in the domain. GeoAc solves the equations governing acoustic propagation through the atmosphere in the geometric limit using a RK4 algorithm.

2.3 Memory Optimization

Memory is a key bottleneck in scienti c computing. Scienti c applications are memory-bound, often requiring large amounts of data from memory. As a result, most of its execution time is spent reading and writing data. Even though microprocessor and memory speed are improving exponentially, the rate of improvement of
microprocessor speed far exceeds that of memory, creating what is referred to as the memory wall [29]. For a a few decades now, processor speed has increased by about 80% per year [14], as opposed to memory speed that has only improved at about 7% per year [11]. This increasing processor-memory performance gap results in the processor spending a significant amount of time, and as a result energy, waiting for data from the memory. As a result, the performance of scientific applications that are memory-bound are significantly impacted.

Memory optimizations include a range of techniques used to optimize memory usage that can then be used to improve the performance of scienti c applications. Loops are a prime candidate for optimization since they may provide a great source for data parallelism. Loop fusion is a compiler optimization and transformation technique
that joins two or more statements from separate loops into a single loop. Read-reduce fusion involves fusing loops that read from the same memory location and provides opportunities to reduce the number of times the same data is read. This results in better data locality. Data locality is the property where references to the same memory location or adjacent locations are reused within a short period of time [15]. Better data locality ensures that the most frequently accessed data can be retrieved quickly. Producer-consumer fusion involves merging loops where one loop writes a variable that is then read by the second loop thereby reducing the temporary storage requirement [6].

2.4 Optimization Frameworks

This section provides an overview of the polyhedral and sparse polyhedral compiler optimization frameworks, and presents the Computation API, a SPF optimization framework that this case study drives.

2.4.1 The Polyhedral Model

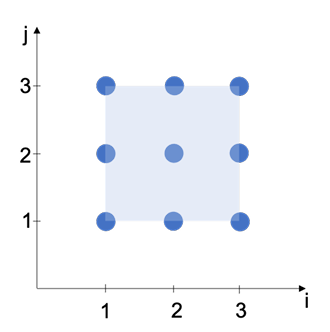
The polyhedral model is a mathematical framework used to represent and manipulate loop nests of programs that perform large and complex operations in a compact form. The iterations of the loop-nest in Figure 2.2 can be represented as lattice points on a polyhedron as shown in Figure 2.3. The associated iteration space is represented graphically as a two-dimensional space (i,j) where each node in the graph represents an iteration. An iteration space that describes a loop nest is considered an a ne space when the lower and upper bounds of each loop can be expressed as a linear function.

A loop nest can be represented with the following components:

• Iteration Domain: The set of executed instances of each statement of the loop. These sets are represented by a ne inequalities.

• Relations: The set of reads, writes, and may-writes that relate statement instances in the iteration space to data locations.
• Dependences: The set of data dependences that impose restrictions on the execution order.
• Schedule: The overall execution order of each statement instance represented by a lexicographically ordered set of tuples in a multidimensional space [9].

A transformation in the polyhedral model is represented by a set of a ne functions, one for each statement, called scheduling functions. An a ne transformation is a linear mapping that preserves points, lines, and planes. A ne transformations can be applied to the polyhedron which is then converted into equivalent but optimized code. This conceptualization enables the compiler to reason about loop transformations as manipulating iteration spaces of loop-nests. A limitation to the polyhedral model is that the constraints within iteration spaces and transformations must be a fine.

2.4.2 The Sparse Polyhedral Framework (SPF)

The Sparse Polyhedral Framework extends the polyhedral model by supporting non-a ne iteration spaces and transforming irregular computations using uninterpreted functions [13]. Uninterpreted functions are symbolic constants that represent data structures such as the index arrays in sparse data formats. Symbolic constants are constant values that do not change during the course of a computation. The SPF represents computations with indirect memory accesses and run-time reordering transformations with integer tuple sets and relations with a ne constraints and constraints involving uninterpreted function symbols [26, 27]. Run-time data reordering

techniques attempt to improve the spatial and temporal data locality in a loop by reordering the data based on the order in which it was referenced in the loop [25].

Sets and Relations in the SPF

At the core of the SPF are sets and relations. Data and iteration spaces are represented with sets, while access functions, data dependences, and transformations are represented with relations [26]. Sets are speci ed as shown in Equation 2.2, where each x is an integer tuple and each c is a constraint. The arity of the set is m, the dimensions of the tuples.

(2.2)

 

The constraints in a set can be either equalities or inequalities which are expressions containing symbolic constants or uninterpreted functions [26].

A relation is a mapping of sets of input integer tuples to output integer tuples. Relations are speci ed as shown in Equation 2.3.

(2.3)

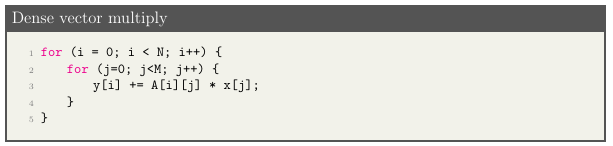
Each x is an input tuple variable, each y is an output tuple variable and c is a constraint. Equation 2.4 represents the iteration domain of the dense matrix vector multiply code show in in Figure 2.4. i and j are the iterators in the 2 dimensions of the set and 0 <=i <N and 0<=j <M are the a ne inequalities or constraints that bind the iteration space.

I = [i j] 0 <=i<N 0<=j <M}  (2.4)

2.4.3 The Computation API

This section describes the Computation API from a workshop paper that has been accepted [21] for publication. This case study contributed to the design and testing of the Computation API. The Computation API is an object-oriented API that provides a precise speci cation of how to combine the individual components of the SPF to
create an intermediate representation (IR). An IR is a data structure used internally by the compiler to represent source code. This IR can directly produce polyhedral data ow graphs (PDFGs) [6] and translates the graph operations de ned for PDFGs into relations used by the Inspector/Executor Generator Library (IEGenLib) [26] to perform transformations.

IEGenLib is a C++ library with data structures and routines that can represent, parse, and visit integer tuple sets and relations with a ne constraints and uninterpreted function symbol equality constraints [26]. The Computation API is implemented as a C++ class in IEGenLib [26] and contains all of the components required to express a Computation or a series of Computations. Dense and sparse matrix vector multiplication, shown in Figure 2.4 and Figure 2.5 respectively, are used as examples to represent the computations in the SPF. The components of a Computation are: data spaces, statements, data dependences, and execution schedules. The proceeding subsections describe the design and interface for each of these components.

Data spaces

A data space represents a collection of conceptually unique memory addresses. Each combination of data space name and input tuple is guaranteed to map to a unique space in memory for the lifetime of the data space. The data spaces represented in the matrix vector multiply examples shown in Figures 2.4 and 2.5 are y, A, and x. In the sparse version the index arrays rowptr and col are also considered data spaces.

Statements

Statements perform read and write operations on data spaces. Each statement has an iteration space associated with it. This iteration space is a set containing every instance of the statement and has no particular order. A statement is expressed as the set of iterators that it runs over, subject to the constraints of its iteration (loop
bounds). A statement is written as a string and the names of the data spaces are delimited with a $ symbol (see lines 2 and 5 in Figure 2.7). The iteration space is specified as a set using the IEGenLib syntax, with the exception of delimiting all data spaces with a $ symbol (see lines 3 and 6 in Figure 2.7).

Data dependences

Data dependences exist between statements. They are encoded using relations between iteration vectors and data space vectors. In the matrix vector multiply examples, the data reads and writes are speci ed as shown in Figure 2.8.

Execution schedules

Execution schedules are determined using scheduling functions that are required to respect data dependence relations. Scheduling functions take as input the iterators that apply to the current statement, if any, and output the schedule as an integer tuple that may be lexicographically ordered with others to determine correct execution order of a group of statements. Iterators, if any, are used as part of the output tuple, indicating that the value of iterators a ects the ordering of the statement. For example, in the scheduling function [i j]
[0 i 0j0] , the position of i before j signifies that the corresponding statement is within a loop over j, which in turn is with in a loop over i.

Figure2.10 shows the complete specification of the dense matrix vector multiply  followed by the sparse matrix vector multiply.

CodeGeneration

Polyhedra scanning is used to generate optimized code. The Computation class interfaces with Code Gen+[4] for code generation. Code Gen+uses Omega set sand

relations for polyhedra scanning. Omega [12] is a set of C++ classes for manipulating integer tuple relations and sets. Omega sets and relations have limitations in the presence of uninterpreted functions. Uninterpreted functions are limited by the pre x rule whereby they must be a pre x of the tuple declaration. Uninterpreted functions cannot have expressions as parameters. Code generation overcomes this limitation by modifying uninterpreted functions in IEGenLib to be Omega compliant. Figure 2.11 shows the results of code generation for the sparse matrix vector multiplication Computation de ned in Figure 2.10. Line 2 of Figure 2.11 defines a macro for the statement s0, lines 7- 9 remap the Omega compliant uninterpreted function back to its original, and lines 11- 16 are a direct result of polyhedra scanning from CodeGen+. The Computation implementation provides all of the supporting definitions for fully functional code.

 

CHAPTER 3

ENGINEERING UPDATE OF GEOAC

This chapter provides details on the software engineering updates performed on GeoAc. The contributions described in this chapter include section 3.1 which de scribes the various steps culminating in the shared memory parallelization GeoAc, performance results as a result of the parallelization in section 3.1.5, and section 3.2,
which details upgrading data formats from a generic data le to industry standard NetCDF format.

3.1 Parallelizing GeoAc

Scientific applications typically run on large clusters/supercomputers. Power is an important design constraint of these machines. The longer an application runs the more power it consumes. A direct result is a requirement for expensive cooling solutions to keep the hardware running optimally. Scienti c applications that are designed to take advantage of parallelism run faster and as a result save time, energy and money.

While GeoAc improved the physics of the generated models, it still wasnt fast enough to be used as a real-time monitoring tool. A serial run on GeoAc with the input parameters as speci ed in Figure 3.5 took approximately 19 hours on Boise States R2 compute cluster. The following sections describe the e ort taken to parallelize GeoAc using OpenMP [5].

3.1.1 Performance Pro ling

Pro ling GeoAc helped identify which parts of the application were expensive, and could be good candidates for a code rewrite to potentially make the application run in parallel. Pro ling tools record what fraction of a programs run-time is spent in various portions of the code. The GNU gprof [8] utility is one such tool that reports this data at function-level granularity. GeoAc was pro led using gprof to generate the call graph seen in Figure 3.1. Each node in the graph represents a function. The rst number is the percent of cumulative time spent in the function
or its subroutines against the total runtime of the application. The second number, listed in parentheses, is the percentage of time spent directly in the function. The third number is the total number of calls to the function.
An open source python script gprof2dot [7] was used to convert the call graph into a dot graph. Graphvizs dot renderer was then used to generate an image of the dot graph. Examination of the dot graph helped us gain an overview of the relationships between the different functions in GeoAc.

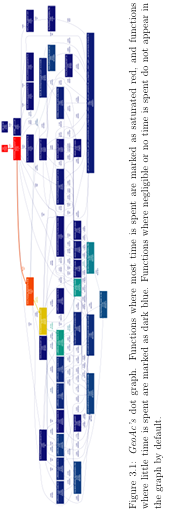
From the dot graph, we were able to identify that a majority of the time spent by the application was in the GeoAcGlobal called the GeoAc Propagate RK4 function. RunProp function. This function in turn

3.1.2 Identify Candidate Loops

Pro ling GeoAc also helped us identify important loops that could be candidates for optimization. A manual analysis of the code revealed the legality of parallelizing expensive sections of the code. Figure 3.3 shows a loop nest within the GeoAcGlobal RunProp function. This seemed to be an ideal target for optimization.

3.1.3 Refactor to prepare for OpenMP

A manual data ow analysis was conducted to determine reads and writes within parallel sections. Any variable written to in the parallel section must be thread local. All global variables that were not constant were refactored and made local so

that every thread has a local copy of the variable. After the data ow analysis, all non-constant global variables were re-declared locally and added as parameters to functions where the globals were being used. In some functions, global structs were being used. Since each thread requires a local copy of the struct, it was rede ned and moved to a header le so that local instances could be called by the driver. In one particular function, a new struct called SplineStruct was created as shown in Figure 3.4, that held all the global variables the function used in order to conveniently pass the required variable around.

3.1.4 Implementation and Testing

After refactoring the code, OpenMP was used to achieve shared memory parallelization. OpenMP consists of a set of compiler directives (#pragmas) and library routines that provides support for parallel programming in shared-memory environments. These directives are designed such that even if the compiler does not support
them, the program will still execute, but without any parallelism. The #pragma omp for directive was applied to the nested loop identi ed in section 3.1.2. The loop construct for speci es that the iterations of loops will be distributed among and executed by the encountering team of threads. By default when OpenMP encounters the #pragma omp for directive, it creates as many threads as there are cores in the system.

3.1.5 Performance

Correctness was ensured by running the application successfully using the following test parameters in Figure 3.5 without any errors or warnings.

Multiple runs of the application were conducted with varying number of threads and a preliminary performance analysis was conducted.

Table 3.1: Performance results of parallelized GeoAc

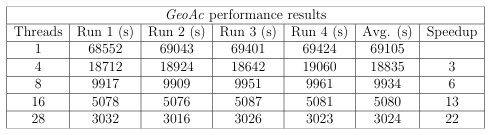
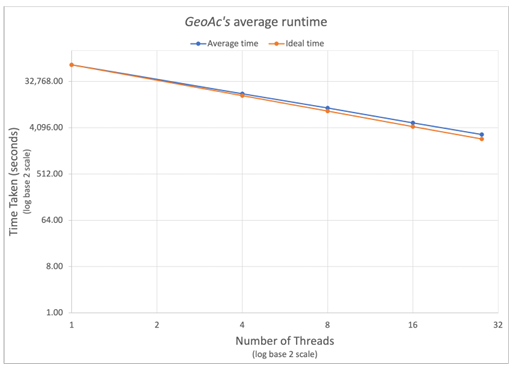
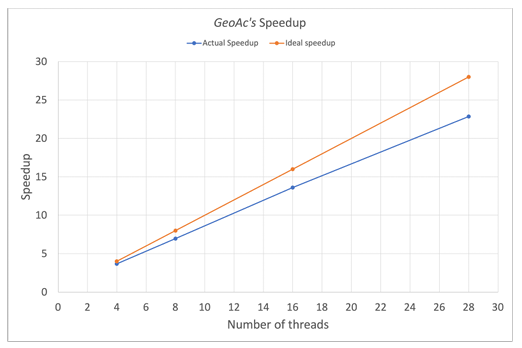
Figure 3.6 shows the average runtime measured over four runs with 1, 4, 8, 16 and 28 threads. For this particular set of input parameters, 28 threads was the clear winner with an average runtime of about 50 minutes as opposed to 19 hours with the serial version. The 28 thread run resulted in a 22x speedup over the serial version of the code as shown in Figure 3.7.

3.2 Upgrading data formats to industry standards

GeoAc outputs data in generic DAT les. One of the problems with this data type is that when GeoAc is run with larger parameter sets, the output les can grow significantly large. Another problem that was discussed earlier in section 2.1, is that the NetCDF format is used to store grid information between each step of IonoSeis. At the request of the domain scientist and in the interest of conforming to IonoSeis and industry standards, the code was modi ed to output NetCDF les rather than generic DAT les.

3.2.1 The Network Standard Data Format (NetCDF)

NetCDF is a machine-independent data abstraction commonly used for storing and retrieving multi-dimensional scienti c data [24]. A NetCDF le contains dimensions, variables, and attributes. These components are used together to describe data fields in a multi-dimensional dataset. A dimension has a name and size and can be
used to represent a physical dimension like the number of rays and the maximum points along a ray. Variables have a datatype, name, and dimension and store the bulk of the data. Attributes are used to provide more information about a particular variable or the NetCDF le in general. Figure 3.8 shows the structure of a NetCDFle generated with GeoAc using the CDL (Common Data Language) notation. CDL is a human-readable notation for NetCDF data.

NetCDFis not thread-safe. As a result, it was not possible to parallelize the le i/o without using locks or some sort of mutual exclusion which would have signi cantly increased the complexity of the implementation. The parallel implementation wrote data les per thread and combined them at the end of the parallel section. Instead of combining each of the threads data les, a better option was to gather the data from each thread and write it directly to a NetCDF file.

 

CHAPTER 4

REPRESENTING GEOAC USING THE SPF

Based on the pro le and a manual data ow analysis of the code, portions of GeoAc that could potentially be expressed using the sparse polyhedral framework were identi ed. The GeoAc Propagate RK4 -2 function was deemed the most suitable. Data and iteration spaces are represented using sets while access functions, data dependences, and transformations are represented using relations. This chapter discusses the development of the optimization framework (Computation API) by incrementally expressing GeoAc code using the SPF and tackling limitations as they arise. From GeoAcs dot graph in Figure 3.2, it is evident that the GeoAc GeoAc Propogate RK4 and GeoAc RunProp, Update Sources functions have the greatest per cent of cumulative time spent in them. The core of the acoustic ray-tracing of GeoAc is performed by an RK4 algorithm, so the GeoAc
Propogate RK4 was deemed most appropriate to represent using the SPF. The strategy of representing the op
erational code with the SPF involved identifying the leaf function called from the GeoAc
Propogate RK4 function and representing it using the Computation API. We work our way upwards from there.
To determine the leaf function, a manual data ow analysis was conducted to identify all the function calls. Each function was traversed iteratively until the leaf func tion is reached. The rst call in GeoAc
function. The GeoAc Propogate RK4 is to the GeoAc Update Sources Update Sources function calls the c function which in turn calls the Eval Spline f function. The Eval Spline f function then calls the Find function which was determined to be the leaf function from a call to the GeoAc It should be noted that the GeoAc
Propogate RK4 function, the GeoAc and the remaining functions were all in di erent compilation units.
After the data ow analysis, the Find Segment Propogate Update Sources Segment function is expressed using the
sparse polyhedral framework. This is done using function inlining with the Computation API described in Section 2.4.3.

4.1 Iterative Development

Iterative transformations are a key goal of the Computation API. Contributions of this thesis evaluate how well the iterative transformations work. We breakdown the SPF representation process into small iterative pieces that are tested with the operational GeoAc code. We start by representing the leaf function Find Segment as a reusable function that returns a Computation which is outlined in Section 4.2. Code generation is called on the Computation with a driver developed in IEGenLib. This results in a C le with compiler generated statement macros. This le is dropped into the operational GeoAc code in place of the Find Segment function as a preprocessor directive (# include). GeoAc is then run on a test case with known results and the new results are compared for correctness.

4.2 Function Inlining

Functions are useful in breaking down programming solutions to smaller reusable modules and help with code structure. They, however, present challenges with inter procedural analysis. Function inlining is an optimization that copies code from the function definition directly into the calling functions code. This eliminates the need
for a separate set of instructions in memory and exposes optimization opportunities. One of the goals of the Computation API is to eliminate the interprocedural analysis challenge.

The c, v and u functions within GeoAc functions- Eval Spline f and Find Update Sources each called two other
Segment. Furthermore, since the parent function GeoAc Update Sources is within a for loop, each of these functions end up being called multiple times. To enable code reuse, functions that return a Computation* were created in the optimization driver wherein each function in the driver corresponds to the SPF representation of the function we were optimizing in GeoAc. The Computation* returning functions are only ever called once. Subsequent calls to a function involved appending the same Computation multiple times. Figure 4.8 shows the leaf function Find Segment Computation.

Nested function calls resulted in the development of the append Computation function shown in Figure 4.1. This function take as its parameters the Computation to be appended (appendee), the iteration domain of the appendee context, the execution schedule of the appendee context and a vector of strings containing arguments to Computation to be appended. The return valued of this function is a Append  Computation Result struct that consists of a vector of strings that holds the return value (name of a dataspace or a literal) of the function that is being appended and an integer that is the depth of the last statement in the appendee.

One of the problems with inlining functions across multiple compilation units was name collisions between the caller and callee functions. The add Parameter function takes as its parameters a pair of strings- the name of the argument and its datatype. Data space renaming prevents name con icts between the caller and callee as well as
multiple invocations of the callee within the same context. This is taken care of by the append Computation function under the hood. The argument is checked for whether it is a data space in the caller, and an exception is thrown if it is not. Literals were initially not supported. The caller is required to assign literals to temporary variables and then pass those variables in as arguments. If a check on the argument indicates that it is not a data space, it is considered a literal and evaluated. Expressions in function calls are not supported. The caller will need to assign the expression to a temporary data space.

Since inlining copies code from the function de nition directly into the calling functions code, return statements are invalid. The append Computation function supports return values by returning a struct which consists of the depth of the last appended statement and a vector of strings that hold the return value (name of a dataspace or a literal). It is the callers responsibility to keep track of whether the return type is a literal or data space.

Our use case necessitated function calls nested within loops. Functions being called within loops of the calling function is a fairly common pattern in scientific applications. In this situation the inlining procedure must adjust the iteration spaces and scheduling functions of the callee to appear within the loop structures. By copying
data from previous computations up to the given depth of the surrounding execution schedule, the inlining procedure was able to support function calls within loops. Figure 4.2 shows a nested function call. The third parameter of the append Computation function on line 13 indicates that a call to aComputation is the rst statement in an i loop (nested function call).

 

4.3 Data-dependent Early Loop Exits

The Find Segment function shown in Figure 4.3 is used to find the segment index as well as evaluate the 1D vertical spline. From the code, and by examining results of debug print statements, it was observed that the function was originally written with a loop optimization. The start, middle and end of the xvals array were checked at the start of the function to quickly calculate the segment index without having to iterate through the entire array. There were multiple data-dependent early loop exits in the code.

Data dependent loops have data dependencies, making parallelization di cult without extensive refactoring. With the function now inlined, data-dependent early exits would cause an early exit in the inlined code resulting in unforeseen errors. As a result of this nding, research is ongoing to add data-dependent early exits and data-dependent control ow in general to the SPF. The Computation API does not at present support data-dependent early exits and as a result, the function was refactored as shown in Figure 4.4.

Figure 4.4: The modi ed Find.Segment function to take care of early exits and return statements

 

Once the Find Segment function was represented in the SPF, we move up to the next one which is the Eval Spline f function. We repeat this process until the code in the function we were originally trying to represent in the SPF is replaced with code generated using the Computation API.

4.4 Rewrite code using the SPF

This section presents operational GeoAc code represented in the SPF using the Computation API. The Computation APIis used to represent the modi ed Find Segment function in Figure 4.5. The rst parameter is the source code within the i loop and is written as a string on lines 1 and 2 of Figure 4.5. The names of the data spaces in the source code are delimited with $ symbols.

Statements have an iteration space associated with them. This iteration domain is a set containing every instance of the statement and is typically expressed as the set of iterators that the statement runs over, subject to the constraints of their loop bounds. The iteration space is represented on line 3 of Figure 4.5 using the IEGenLib syntax with the exception of wrapping data spaces with the $ sign. Equation 4.1 represents the iteration space of the Find Segment function.

I = [i] i>=0 i<length}      (4.1)

As discussed in Section 2.4.2, constraints to an iteration space should be provided as symbolic constants. An interesting case that we came across is when constraints were passed in as arguments to the function. By default, adding parameters to a Computation also added them as data spaces to the Computation. It was necessary
to identify variables that are never written to and make sure that they arent renamed. Data dependences are encoded using relations between iteration vectors and data space vectors. The data reads and writes can be specified as shown in Figure 4.6: Execution schedules are determined using scheduling functions. They take iterators that apply to the current statement as the input, if any, and output the schedule as an integer tuple that may be lexicographically ordered with others to determine

correct execution order of a group of statements. Figure 4.7 shows the execution schedule of the Find Segment function.

Once we have all the di erent components of a Computation, we can specify the full Computation as Figure 4.8. The Computation class interfaces with CodeGen+ for code generation. Calling codegen on a Computation generates C code in the form of statement macros and calls to them. A macro is a fragment of code which has
been given a name. Whenever the macro name is used, it is replaced by the contents of the macro. Figures 4.9 and 4.10 shows the result of code generation.

 

 

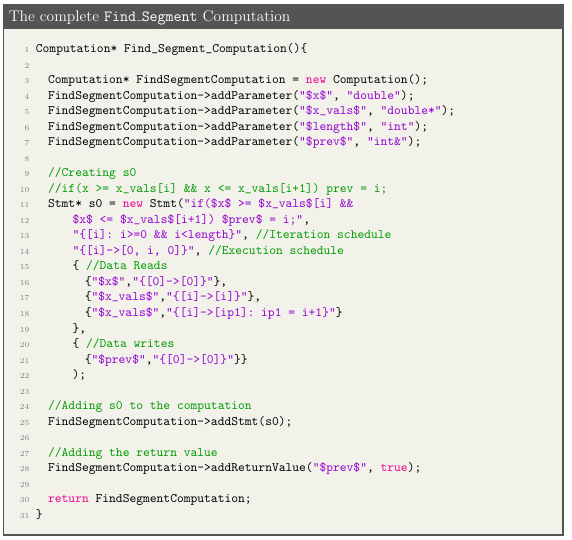
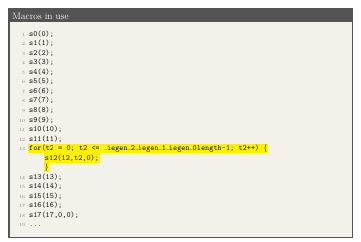
Figure 4.10: Calls to the macros de ned in Figure 4.9.Line 13 represents the call to the Find. Segment function.

 CHAPTER 5

RELATED WORK

5.1 Applying polyhedral optimizations to scientific applications

Polyhedral Data ow Graphs (PDFG) are a compiler internal representation that exposes optimization opportunities such as loop transformation and temporary storage reductions. To implement PDFG, the framework introduces a speci cation language called Polyhedral Data ow Language (PDFL). This speci cation language can be written directly, derived from existing codes, or lifted from another intermediate representation.

Existing work demonstrates the bene t of polyhedral data ow optimizations. Olschanowsky et al. demonstrated this bene t on a computational uid dynamic (CFD) benchmark [20]. Davis et al. automated the experiments from the previous work using modi ed macro data ow graphs [6]. Strout et al. extended the polyhedral model for sparse computations allowing indirect array accesses [26]. This research distinguishes itself by being applied to a full application in a di erent domain.

Tools such as Polly [10], Pluto [3], Loopy [19], PolyMage [18] and Halide [22, 23, 17] use the polyhedral model to transform regular codes. PolyMage and Halide are two domain speci c languages and compilers for optimizing parallelism, locality, and recomputation in image processing pipelines. Halide separates the de nition of the
algorithm from the concerns of optimization making the algorithms simpler, more modular and more portable. This lets us play around with di erent optimizations with a guarantee not to change the result. PolyMages optimization strategy relies primarily on the transformation and code generation capabilities of the polyhedral compiler framework and performs complex fusion, tiling, and storage optimization automatically. The isl (integer set library) is a thread-safe C library for manipulating sets and relations of integer tuples bounded by a fine constraints [28]. This library is used in the polyhedral model for program analysis and transformations and forms the basis for a fine transformations used in all the tools discussed previously in this section.

CHAPTER 6

CONCLUSION

This thesis presents a case study to represent the GeoAc acoustic ray-tracing tool using the sparse polyhedral framework. GeoAc more accurately models wave propagation phenomena as compared to the current ray tracing tool used in the IonoSeis modelling package. GeoAc was customized to meet the needs of IonoSeiss work ow. OpenMP was used to parallelize GeoAc which resulted in a 22x speedup over the serial version of the code. The run-time went down from about 19 hours to just under 51 minutes for a large set of input parameters.

The parallelized GeoAc code drives the development of a SPF optimization frame work called the Computation API. The leaf functions of the GeoAc codebase were incrementally expressed in the SPF using the Computation API and code was generated as statement macros. These macros were used to replace the leaf functions and the application was run on a set of test parameters to determine the correctness of the results. Each iterative expression of the code in the SPF presented new challenges which helped drive the development of the optimization framework.

 

REFERENCES

[1] Martha L. Abell and James P. Braselton. 2- rst-order ordinary di erential equations. In Martha L. Abell and James P. Braselton, editors, Di erential Equations with Mathematica (Fourth Edition), pages 45131. Academic Press, Oxford, fourth edition edition, 2016.

[2] P Blom. Geoac: Numerical tools to model acoustic propagation in the geometric limit. https://github.com/LANL-Seismoacoustics/GeoAc, 2014.

[3] Uday Bondhugula, J. Ramanujam, and P. Sadayappan. PLuTo: A Practical and Fully Automatic Polyhedral Program Optimization System. PLDI 2008- 29th ACM SIGPLAN Conference on Programming Language Design and Implementation, pages 115, 2008.

[4] Chun Chen. Polyhedra scanning revisited. Proceedings of the ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI), pages 499508, 2012.

[5] Leonardo Dagum and Ramesh Menon. Openmp: an industry standard api for shared-memory programming. IEEE computational science and engineering, 5(1):4655, 1998.

[6] Eddie C Davis, Michelle Mills Strout, and Catherine Olschanowsky. Trans forming loop chains via macro data ow graphs. In Proceedings of the 2018 International Symposium on Code Generation and Optimization, pages 265277. ACM, 2018.
[7] Jose Fonseca. Gprof2dot: Convert pro ling output to a dot graph,.

[8] Susan L. Graham, Peter B. Kessler, and Marshall K. McKusick. Gprof: A call graph execution pro ler. 39(4):4957, April 2004.

[9] Tobias Grosser, Sven Verdoolaege, and Albert Cohen. Polyhedral ast generation is more than scanning polyhedra. ACM Transactions on Programming Languages and Systems (TOPLAS), 37(4):12, 2015.

[10] Tobias Grosser, Hongbin Zheng, Raghesh Aloor, Andreas Simburger, Armin Gro linger, and Louis-Noel Pouchet. Polly- Polyhedral optimization in LLVM. Proceedings of the First International Workshop on Polyhedral Compilation Techniques (IMPACT 11), page None, 2011.

[11] John L Hennessy and David A Patterson. Computer architecture: a quantitative approach. Elsevier, 2011.

[12] Wayne Kelly, Vadim Maslov, William Pugh, Evan Rosser, Tatiana Shpeisman, and David Wonnacott. The omega library interface guide. 1995.

[13] Alan LaMielle and Michelle Mills Strout. Enabling code generation within the sparse polyhedral framework. Technical report, Technical Report CS-10-102, 2010.

[14] John D McCalpin. A survey of memory bandwidth and machine balance in current high performance computers. IEEE TCCA Newsletter, 19:25, 1995.

[15] Kathryn S. McKinley, Steve Carr, and Chau-Wen Tseng. Improving data locality with loop transformations. ACM Trans. Program. Lang. Syst., 18(4):424453, July 1996.

[16] Thomas Mikesell, Lucie Rolland, Rebekah Lee, Florian Zedek, Pierdavide Cosson, and Jean-Xavier Dessa. Ionoseis: A package to model coseismic ionospheric disturbances. Atmosphere, 10(8):443, Aug 2019.

[17] Ravi Teja Mullapudi, Andrew Adams, Dillon Sharlet, Jonathan Ragan-Kelley, and Kayvon Fatahalian. Automatically scheduling halide image processing pipelines. ACM Transactions on Graphics (TOG), 35(4):83, 2016.

[18] Ravi Teja Mullapudi, Vinay Vasista, and Uday Bondhugula. Polymage: Automatic optimization for image processing pipelines. In ACM SIGARCH Computer Architecture News, volume 43, pages 429443. ACM, 2015.

[19] Kedar S. Namjoshi and Nimit Singhania. Loopy: Programmable and formally veri ed loop transformations. Lecture Notes in Computer Science (including subseries Lecture Notes in Arti cial Intelligence and Lecture Notes in Bioinformatics), 9837 LNCS(July):383402, 2016.

[20] Catherine Olschanowsky, Michelle Mills Strout, Stephen Guzik, John Lo eld, and Je rey Hittinger. A study on balancing parallelism, data locality, and recomputation in existing pde solvers. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, pages 793804, 3 Park Ave, New York, NY, USA, 2014. IEEE Press, IEEE Press.

[21] Tobi Popoola, Ravi Shankar, Anna Rift, Shivani Singh, Eddie Davis, Michelle Strout, and Catherine Olschanowsky. An object-oriented interface to the sparse polyhedral library. In 2021 Ninth Workshop on Data-Flow Execution Models for Extreme Scale Computing, Accepted.

[22] Jonathan Ragan-Kelley, Andrew Adams, Sylvain Paris, Marc Levoy, Saman Amarasinghe, and Fredo Durand. Decoupling algorithms from schedules for easy optimization of image processing pipelines. 2012.

[23] Jonathan Ragan-Kelley, Connelly Barnes, Andrew Adams, Sylvain Paris, Fredo Durand, and Saman Amarasinghe. Halide: a language and compiler for optimizing parallelism, locality, and recomputation in image processing pipelines. ACM SIGPLAN Notices, 48(6):519530, 2013.

[24] R. Rew and G. Davis. Netcdf: an interface for scienti c data access. IEEE Computer Graphics and Applications, 10(4):7682, 1990.

[25] Michelle Mills Strout, Larry Carter, and Jeanne Ferrante. Compile-time composition of run-time data and iteration reorderings. SIGPLAN Not., 38(5):91102, May 2003.

[26] Michelle Mills Strout, Geri Georg, and Catherine Olschanowsky. Set and relation manipulation for the sparse polyhedral framework. In International Workshop on Languages and Compilers for Parallel Computing, pages 6175. Springer, 2012.

[27] Michelle Mills Strout, Alan LaMielle, Larry Carter, Jeanne Ferrante, Barbara Kreaseck, and Catherine Olschanowsky. An approach for code generation in the sparse polyhedral framework. Parallel Computing, 53:3257, 2016.

[28] Sven Verdoolaege. isl: An integer set library for the polyhedral model. In International Congress on Mathematical Software, pages 299302. Springer, 2010.

[29] Wm. A. Wulf and Sally A. McKee. Hitting the memory wall: Implications of the obvious. SIGARCH Comput. Archit. News, 23(1):2024, March 1995.

[30] L. Zheng and X. Zhang. Chapter 8- numerical methods. In Liancun Zheng and Xinxin Zhang, editors, Modeling and Analysis of Modern Fluid Problems, Mathematics in Science and Engineering, pages 361455. Academic Press, 2017.

 

APPENDIX A

EXPERIMENTAL SETUP

The work in this thesis has been developed and tested on the R2 high performance cluster at Boise State University. Each node on the cluster is a dual socket, Intel Xeon E5-2680 v4 CPU at 2.40 GHz clock frequency. Each node consists of two Non-Uniform Memory Access (NUMA) domains each containing 14 cores. Each core has its own local memory and each node is connected with one another by means of high speed interconnect links. The cores include a 32KB L1, 256KB L2 cache. In addition, each core has access to a shared 35MB L3 data cache in each NUMA domain. Figure A.1 shows the CPU architecture information as a result of the lscpu command.